ぞっくま別解では、常識的な解法は求めません。
一般的な試験や受験では、常識が求められる場合がほとんどです。
ぞっくま別解は、試験や受験の参考にはなりません。
問題
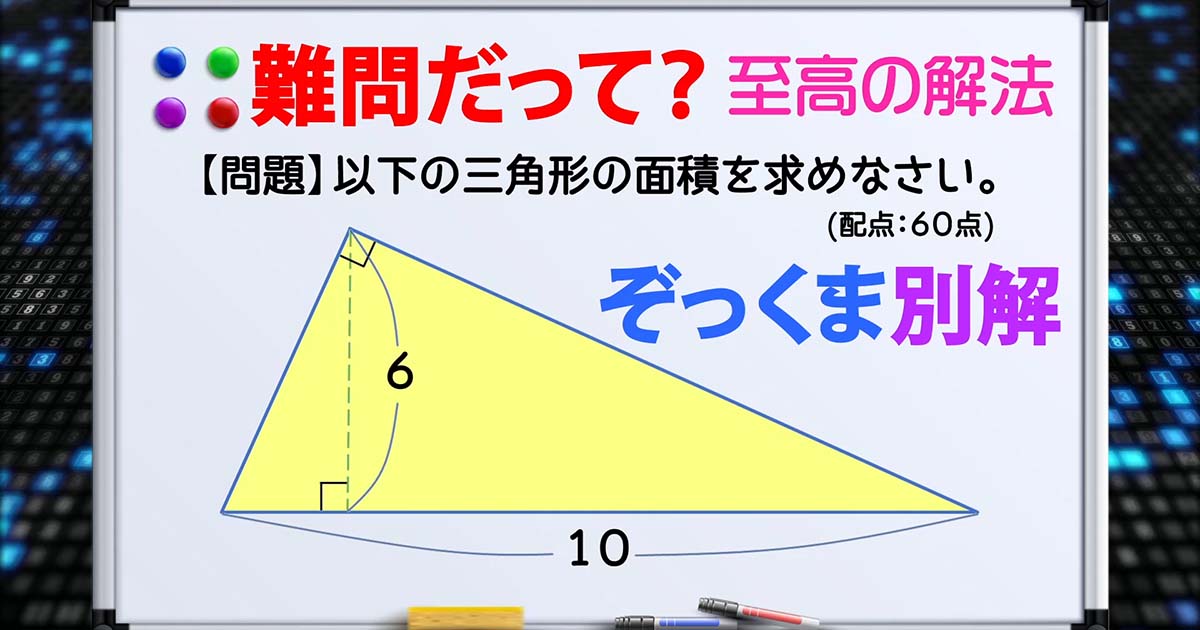
以下の三角形の面積を求めなさい。
配点: 60点
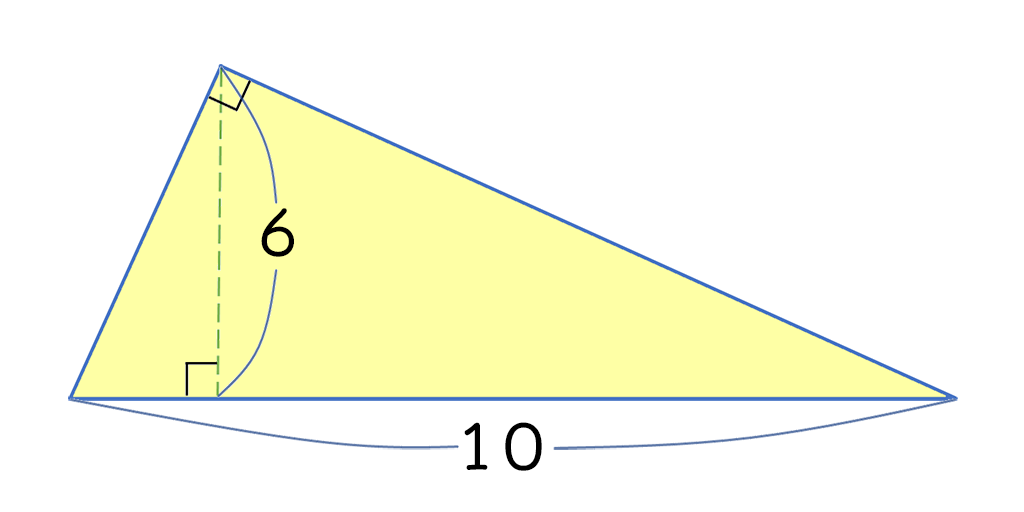
解答例(ぞっくま別解による特殊解答)
\(三角形の絵の中の数値は、\\
n進数表記(nは自然数)である\\
と理解しました。\)
\(高さ部分は、6であるので、\\
一般的なアラビア数字であるとすると、\\
n \ge 7 となります。\)
\(10進数のdを(d)_{10},\\
n進数のmを(m)_nと表記することとします。\)
\(\begin{align*}
(10)_n & = (1 \cdot n + 0)_{10}, \\
(6)_n & = (6)_{10}なので、
\end{align*}\\
与えられた三角形の面積を\\
10進数で計算すると、\\
\displaystyle\left(\frac{n \cdot 6}{2}\right)_{10} = (3 \cdot n + 0)_{10}.\)
\((3 \cdot n + 0)_{10} = (30)_nであるので、\\
三角形の面積は、n進数で30となります。\)
\(ここで以下のような図形を考えます。\)
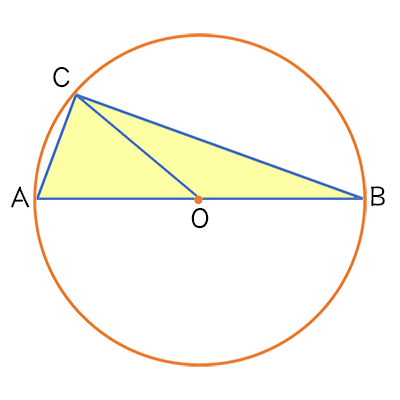
\(線分ABを直径とする円を考えて、\\
点Cは、その円上の点とします。\\
(ただし、点Cは、\\
点A、点Bと異なる点とする。)\\
線分ABの中点をOとすると、\\
Oは円の中心となります。\)
\(\triangle{ABC}, \triangle{AOC}, \triangle{BOC}\\
を考察していきます。\)
\(OA, OCは円の半径なので、\\
\triangle{AOC}は、OA = OCとなる\\
二等辺三角形になります。\\
よって、\angle{OAC} = \angle{OCA}.\\
\angle{OCA} = \alphaとおくと、\\
三角形の内角の和は180^{\circ}なので、\\
\angle{AOC} = 180^{\circ} – 2\alphaとなります。\)
\(同様にして、\\
二等辺三角形\triangle{BOC}を考えると、\\
\angle{OBC} = \angle{OCB}.\\
\angle{OCB} = \betaとおくと、\\
\angle{BOC} = 180^{\circ} – 2\beta.\)
\(\angle{AOC} + \angle{BOC} = 180^{\circ}なので、\\
\begin{align*}
(180^{\circ} – 2\alpha) + (180^{\circ} – 2\beta) & = 180^{\circ}\\
2\alpha + 2\beta & = 180^{\circ}\\
\alpha + \beta & = \ \ 90^{\circ}.\\
\end{align*}
\)
\(\alpha + \beta = \angle{OCA} + \angle{OCB}なので、\\
\angle{ACB} = 90^{\circ}となります。\)
\(よって、\triangle{ABC}は、\\
\angle{ACB}を直角とする、\\
直角三角形になります。\)
\(以下の図のような、\triangle{AOC}が直角になる\\
特殊な例を考えます。\)
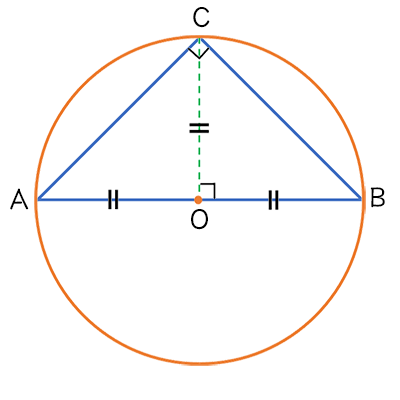
\(点Cから線分ABに対して\\
垂直に下ろした交点をHとすると、\\
上の図の場合は、\\
H = Oとなり、CH = COとなります。\)
\(点A、点Bとは異なる円上の点C^{\prime}と、\\
そこから線分ABに対して\\
垂直に下ろした交点H^{\prime}を考えると\\
C^{\prime}H^{\prime} \le CHとなる。\)
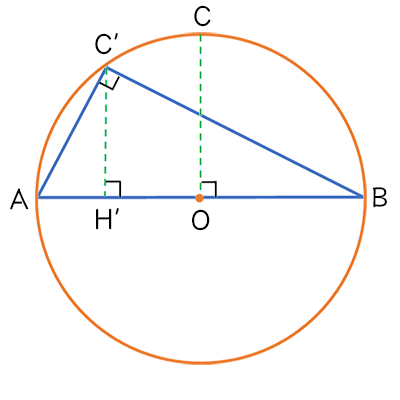
\(また、AB = 2 \cdot CHであるから、\\
2 \cdot C^{\prime}H^{\prime} \le AB.\)
\(ここまでの考察と、\\
問題で与えられた三角形を考慮すると、\\
底辺の(10)_nは、\\
高さ(6)_nの2倍以上である必要がある。\\
\begin{align*}
(1 \cdot n + 0)_{10} & \ge (2 \cdot 6)_{10}\\
(n)_{10} & \ge (12)_{10}なので、\\
n & \ge 12.
\end{align*}\)
\(以上から、求める三角形の面積は、\\
n進数で30.\\
ただし、nは、n \ge 12となる自然数。\)
これが、ぞっくま別解の解答となります。
解答の解説
解答例では、なにやら、
いきなりn進数で面積を求める →
三角形の存在条件を検討する
という順番で解いています。
これは自然な順番ではありません。
本来であれば、
三角形の存在有無に関する議論 →
n進法なら求められるという結論 →
実際にn進数で面積を求める →
三角形の存在条件の検討
の順番が自然な順番だと思います。
今回は、倒置的な技法を使って、自然ではない順番で解くことによって、
解答に躍動感を与えようと試みています。
三角形の内角の和が180度であることなどは、
解答中では、常識であるという前提で証明なしで扱っています。
どこまで詳細に証明して使うかは、適当な判断が必要だと思いますが、
今回は問題の本質ではない部分は、常識として扱っています。
n進法に関しても、特に深い議論はなしに、一般論として使っています。
状況(この問題にかけられる時間など)によっては、
円と直角三角形の関係の部分も、
詳細な考察なしに、常識として扱っていいかもしれません。
解答の課程で、n進数を10進数に直してから解いていますが、
これは説明的な解答を試みるために、敢えて、そうしています。
解答は、見る人とのコミュニケーションなので、
相手により納得してもらいやすい手順を書こうとの試みになります。
実際には、n進数での10は、ちょうど桁上がりした数値なので、
10進数に直さずとも、
「三角形の面積は、n進数で30」という結論は、
すぐに導くことは可能です。
αとβが出てくるくだりでは、以下のような考察で
直角三角形になると導いてもいいと思います。
どちらの手順がはじめに頭に浮かんだかによりますが、
以下の方が計算は楽かもです。
ぼくは先に解答例の手順を思いついて、結論出すところで、
こっちの方が早いじゃんと思いついた感じです。
\(\triangle{ABC}について、\\
\angle{ACB} = \alpha + \betaについて考えます。\\
三角形の内角の和は180^{\circ}なので、\\
\alpha + \beta = 180^{\circ} – (\alpha + \beta).\\
これを計算すると、\\
\alpha + \beta = 90^{\circ}.\)
ちなみに、ぼくは、普段は弧度法(ラジアン)を愛用しているので、
○○度の表記は久々に使用して、記号がこの書き方でよかったかと
ちと心配です(間違ってたらごめん)。
解説動画
総評
16進数などの特定のものに限定せず、
一般化したn進数として面積を求め、
nの条件に関しても議論できた点は良かったと思います。
ぼくが求める解答に対する躍動感や美しさという点に関しては、
まだ物足りなさが残ります。


コメント